Hauling systems, free body diagrams, forces--help!

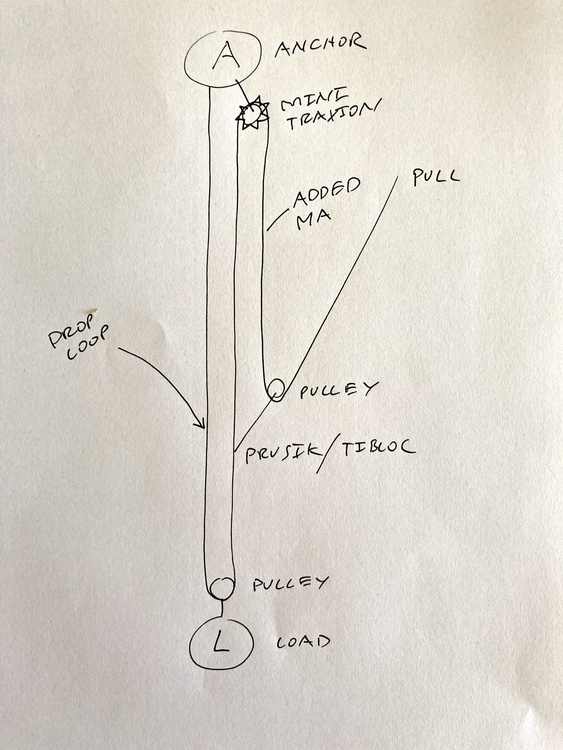
Hi Folks, 

The recent thread about crevasse rescue techniques (https://www.mountainproject.com/forum/topic/124662117/critique-this-crevasse-rescue-method#ForumMessage-124694651) sent me down a black hole.

I've drawn some basic diagrams and played with some numbers.  Can folks with more knowledge than I check my approach and calculations?

I'm starting really basic, but please bear with me.

1-My general method for crevasse rescue is a drop loop C with a Z drag added.  I think that the theoretical mechanical advantage of the drop loop is 2:1 and the Z drag is 3:1 so for the whole system it would be 5:1.  Is that correct?  Here's a picture of the basic system. 

2-I would like to understand the forces involved when hauling.  For example, if pull on the haul line with force X, how much force will be applied to the load, how much will be supported by the anchor, and how much force will each strand bear?  This might not be the best way to think about these things, but it gives me a starting point.  Is there a better way to approach this analysis?

3-In the system I have pulleys and a microtraxion.  For my calculations I have assumed the pulleys and microtraxion are 80 % efficient.  So if I take a pulley and pull on one strand with force X then the other strand will experience a force of 0.8.  To calculate the force on whatever the pulley is attached to it would be the sum of the forces on the two stands: 1 + 0.8 or 1.8.  Is that correct?

4-I am note sure how to caculate the forces on the different strands.  Essentially, using the method above, I've tried to calculate the force on a strand going "into" a pulley, the force on a strand coming "out" of a pulley, and to get the force on whatever the pulley is attached to (another stand, the load, the anchor) I've summed the forces on both strands.  Do these numbers look right?

5-I have not taken into account the rope stretch, friction over the lip of the crevasse, or static and dynamic friction.  

6-If this approach is roughly correct, I will try to apply the same reasoning to a situation where you are not hauling but simply holding the load.  In this case, you do not need to take efficiency and friction into account, correct?

OK, that's all for now.  

1- what you show is a 6:1 theoretical system. Use 100% efficiency to calculate it and you'll see that the force pulling up on the load is 6x (where you currently shoe 4.41x). You multiply 2 x 3 to get 6. Think about it like this: the 3:1 multiplies your force by 3. Then you use the 2:1 drop c to multiply that force by 2. Thus 6:1 theoretical advantage.

2- your analysis looks good

3- yes, sans friction lost to the snow surface, which is minimal aside from at the lip.

4- summing is correct. I think the rope stretch can reduce the effectiveness of a force acting "behind" another force, since the stretch will be different. But I haven't thought it through fully and maybe it doesn't have an effect once the stretch is fully taken out.

5- friction over the lip does matter but only for the bottom part of the dropped loop. You can add a "node" on each line of the drop c to represent the lip and assume a friction loss just like you did at the pulleys. If you want to. I wouldn't worry about static vs dynamic since the friction losses are a very rough estimation to begin with. Obviously static friction will be more but how much more? Unknown. The difference may be lost in the significant digits.

6- friction still comes into play when just holding the load. It might be a different number but there is friction acting at each node at all times. Friction exists whenever there is a normal force on the rope, regardless of whether the line is moving. 

Thank you so much for your thoughts Drew, I appreciate it.  

I was going back and forth abotu whether or not two MA systems are additive or multipicative -- thanks for setting me straight. 

My follow up question concerned taking the lip into account, and you answered that. 

One cool thing with this aproach is that you add a load (80 kg, 100 kg, 120 kg, whatever) and then determine how much force you would need to haul that load, and what the anchor would say. 

Rough estimate of course, but perhaps still informative/usefull.

Thanks again.  MP rocks.  

Bruno

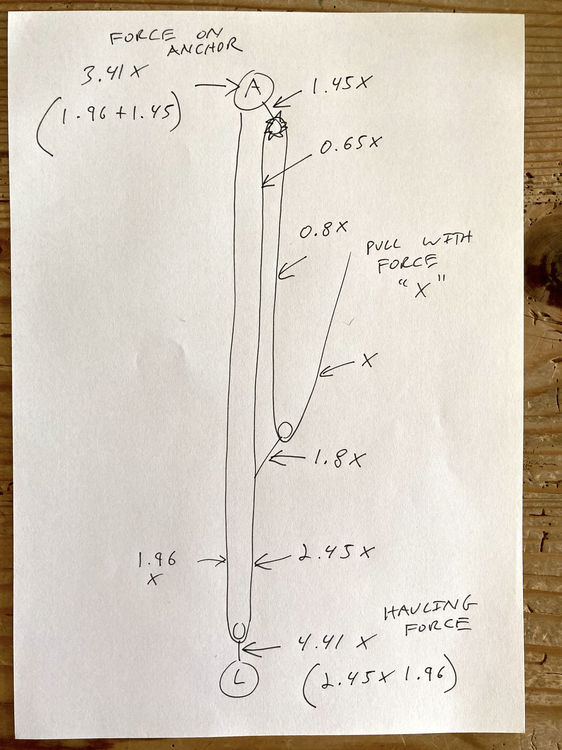
Yes in this case, the load must be less than 4.41x for you to be able to move it if you can only pull with a force of x.

The diagram you're showing is more of a "how much force can I, the rescuer, impart on the fallen climber/anchor" rather than "what is the force on the fallen climber/anchor.

Just remember that the maximum force seen by the anchor is related to both the load and how hard you can pull. The harder you pull, the greater the value of x will be, the faster your load will accelerate up, and the higher the force on the anchor will be. 

Also when the trax engages as you reset, the force on the anchor is the same as the Load, less lip friction.

Once you start pulling again, you accelerate the fallen climber up and that's your max force. After the initial acceleration, if you can pull with a perfectly constant speed, then you'll minimize the force on the system. Hard to do and your anchor better have more margin than needing to do that perfectly. 

OK, follow up question. 

Let's say we have a system with a 4:1 MA.

We have taken into account the efficiency of the various components and edge friction, and we have decided to ignore rope stretch, as above.

The load is 100 kg.

To hold the load in place we would need to pull on the haul strand with 25 kg.  Is that correct?

If we pulled on the haul strand with 26 or 27 kg the load would start to move.  Is that correct?   

The reason I ask is the following.  Using the system above, where you start with an input of "X" on the haul strand, and caculate the forces on all the components, you can divide the load by the mechanical advantage and obtain the minimum value of x required to hold the load in place.  

I assume that to move the load you need to apply a force greater than x. 

Just want to make sure I'm not missing something. 

I know I'm taking liberties here with mass, force, static and dynamic friction, rope stretch, and so on, but I hope the theoretical question is clear.  

All best.

(FYI- kg is not a unit of force but I'm going to use it here just to keep consistent with the 100 kg load you proposed)

Yes you are correct. Again talking purely theoretically:

An object is in static equilibrium when the forces sum to zero and the relative velocity is zero. In the case you made were your'e just holding the load in place: you pull up with 25kg, the anchor pulls up with 75 kg, and the load pulls down with 100 kg. Sum of those is 0 kg and since the load is not moving, we have static equilibrium. 

The system will no longer be in static equilibrium once you start hauling. You will impart additional force on your end of the strand, which will increase the force that the anchor is pulling with. Let's say that's 30 kg. The anchor will now pull with 90 kg. Total load pulling up is 120 kg. The load stays at the same 100 kg, which means the sum is no longer zero. The load will accelerate upwards. You are no longer in equilibrium.

Now this not-in-equilibrium state will only last so long. Once you accelerate yourself away from the lip, and thus accelerate the load up toward the lip, you'll likely stop accelerating as you reach a walking pace that you can maintain, a constant velocity (reminder that we're ignoring friction losses). Once you stop accelerating, so will the load. Now you and the load are moving at a constant velocity. When an object is moving at a constant velocity and the loads sum to zero, it is considered in dynamic equilibrium. So even though the load is moving up, it's still being pulled up with only 100 kg (because neither of you are accelerating because the rescuer is walking at a constant speed now). The only way for it to stop is for the force from above to reduce (rescuer slows down), momentarily, so that the fallen climber can decelerate to a stop, and then be back to a state of static equilibrium.

Just remember that in a real system, you're always losing force to friction/heat. While the theoretical static equilibrium case is a very good approximation of the real world stationary case, this is likely not the case for the dynamic equilibrium case. In a hauling situation, where we can theoretically talk about a dynamic equilibrium, you will actually be pulling with probably much more than 25 kg to keep the system in dynamic equilibrium because of all the losses you'll have due to friction and heat generation at each pulley and lip of the crevasses. It's also near impossible to maintain a perfectly constant pulling speed so you will be constantly accelerating/decelerating yourself and the fallen climber. 

This conversation has evolved/devolved into a basic physics discussion but the real takeaway here is that the maximum force that your anchor will see is either when the microtraxion is locked and the anchor is holding the full load statically (the rescuer is not pulling), or when the rescuer just starts to pull and adds significant force to the system to both accelerate the fallen climber upwards and break static friction that exists throughout the system. I don't know what value this is, but I'd really want my anchor to, at a bare bare bare minimum, be confidently good for 3x the load hanging from it. And ideally 4, 5, maybe 6x the load hanging from it for a margin of safety. With a screw anchor in good glacial ice, that's easy. But things get more questionable with pickets/deadmen. There are some tests that show surprisingly good results from pickets and deadmen, but obviously this will all depend on the snow you have and how well you can build that anchor while holding on to your buddy who's in the crevasse. I love having a team of 3 on a glacier because you can spend the time to build a super bomber anchor and then keep one person in place to back up the anchor. 

Luckily for me, most of the crevasse issues I've had have been in small hidden cracks and someone only falls through until their backpack catches them. Hopefully that remains the case. 

Bruno, you are asking some great questions, so thanks for starting this thread.

I have a couple of suggestions.

1. On my website alpinesavvy.com there is a substantial section on mechanical advantage. I tried to keep things very simple for people who are just getting introduced to the topic and not go too far into the weeds with the engineering stuff. If you're fairly new to this topic, I think this is a good introduction.  https://www.alpinesavvy.com/mechanical-advantage
2. I recently found some excellent YouTube videos that talk about how to use "T method" for figuring out both the theoretical and calculated mechanical advantage of different systems. I've seen lots of other attempts at teaching this material, and for me, these were the best. There are two different videos from the same person (Rescue Craft), part one and part two. You can search YouTube for: "Mechanical Advantages: Counting Tensions and Estimating System Efficiency Part 1".Or, here are the direct links.
3. https://www.youtube.com/watch?v=GKWXIHIcF4o
4. https://www.youtube.com/watch?v=x1FSdt3_Nlc

The problem with calculating system efficiency (and thus the loads or forces) is knowing the efficiency of a bearing in the static condition and when the condition changes since not all of the blocks start moving at the same time or even speed. The same goes for the fibers in the rope which has a huge effect on it's bending resistance. Actually building the system and testing it is the only way to find out as we know from experience, there are just too many variables to make even a vague guess.

This is a great conversation.  The depth of knowledge and generosity on MP is awesome.  

@ Drew--Your explanations are superlative.  I really appreciate such clear and rational ideas.  Are you a teacher?

@ John--Thanks for the links and eveything you do with Alpine Savvy.  I've learned a great deal from the site.  I will study the links you provided. 

@ Jim--You speak the truth (as usual with such topics).  It makes me wonder how much moisture and temnperature effect rope pliability.  I wish I had a test set-up to try it all out just to satisfy my curiosity.  In the absence of such resources, I'm left with imperfect calculations.

I've done some work, and I have two specific questions, but first a quick review.  

I'm considering a drop loop C with an added Z drag.  Theoretical MA is 6:1. I made a pretty picture :)

As I explained above, I wanted to figure out the forces involved when hauling.  For example, if pull on the haul line with force X, how much force will be applied to the load, how much will be supported by the anchor, and how much force will each strand bear?  

To calculate these things, I started with force X on the haul line, and then worked my way through the system, taking into account the efficiency of the pulleys, the progress capture device, the edge friction, and so on.  I did not take into account rope stretch, different rates of hauling, static vs dynamic friction, and so on, although I understand these have an important effect.

The results seem reasonable.  Using an efficiency of 80% for the pulleys, the progress capture device, and the edge friction, I obtained a MA of about 3.5 to 1. That's in line with what I've read elsewhere.

I was then able to solve for X (so to speak) and obtain the force needed to hold the load.  With a 100 kg load the force required is about 28.5 kg and the force on the anchor is about 76.5 kg (I know I am conflating force, mass etc. but I need to keep it simple in my mind). So, theoretically, you would need to pull with more than 28 kg of force to raise the load.

I made a model in Excel where you can change the efficiency of the devices, the edge friction, and the load, and see how the forces change.  This is cool, because you can see why it makes sense to put a high efficiency pulley as close as possible to the haul strand, how low efficiency pulleys can actually reduce forces on anchors, and so on.  The biggest lesson is just how much the pulleys and other device reduce MA.  I would be happy to share the Excel model if anybody is interested.  It would also be relatively easy to create similar models for other haul systems.

Here are my new questions:

I'd like to go the "other way" and calculate the force on the anchor for a given hauling force and load.  My model tells me that hauling with force X will put about 2.6 that amount of force on the anchor, but that does not take the load into account.  To put it another way, in my model I can input the load and it will tell me the force required to hold that hold and the force on the anchor, but I cannot input a hauling force and work backward to the force on the anchor.  

As a first step, I drew a diagram of the system holding a load as if you simply fixed the haul line in place.  I'm having trouble figuring out the load each strand would bear and what the force would be on the anchor.  I think that the anchor would bear the full load 1:1 and the second point where the haul line is fixed would bear half the load but this seems wrong. So that's my first question. Given a drop C with a Z drag and the haul line fixed to a second point, how much of the load would the anchor bear, and how much of the load would the second point bear, and how do you caculate this?

Let's say we find a number for the above situation.  In this hauling system the load will place a particular force on the anchor.  How can I incorporate this force into my model?  Is everything additive? For example, the model said that hauling will place about 2.6 times the force on the anchor.  Can I simply the force from hauling to the force the load places on the anchor?

I hope that makes sense.  

Once again, thank you for the thoughtful contributions. 

In any system hauling from above the load on the anchor is always the load force minus the hauling force no matter what is in between.

Ha I'm definitely not a teacher. Thanks though.

You should be able to calculate the hauling load, theoretically, just the same as you have done already. As long and you remember that for the dynamic system, the theoretical deviates much more from reality than it does with the static system.

Like I had said before, your fallen climber will move as long as you, at least initially, pull with a force greater than that which they are pulling down in the static case (again we're ignoring a lot of things here). Simply pick a hauling force, that when multiplied by your MA, is greater than the load. You do not need to add the weight of the fallen climber into this. It's already built in.

My model tells me that hauling with force X will put about 2.6 that amount of force on the anchor, but that does not take the load into account.

Your model does already take the load into account. Remember, you would not be able to place that force x on the rope if there was nothing there to oppose it. So the load is already in the model.

You can do this pretty cleanly by setting up your calc where you initially input the fallen climber weight, L. Then we arbitrarily input a factor for what we thing it will take to break static friction and accelerate them initially. Let's say that's 1.5L (I made this up, there's very little you can do other than real world testing with a high frequency load cell to figure out what this really is). 

I obtained a MA of about 3.5 to 1

Ok so you can pull with force x. So if you want to apply 1.5L, you'll need to pull with (1.5/3.5)L. Input that as x in your model and there you go. That should tell you what force your fallen climber feels and what force the anchor feels the moment you start pulling.

I still think this is very likely way off from reality. It's just not easy to consider everything that happens in a complex dynamic system like this without a more robust model. Testing different scenarios would be much more efficient and trustworthy. But the theoretical exercise is fun regardless, as long as you know that you probably want a factor of safety of 3. or even more, on whatever you think the anchor force is. 

Jim Titt wrote:

In any system hauling from above the load on the anchor is always the load force minus the hauling force no matter what is in between.

This isn’t accurate. Consider an MA system with a single anchor that also includes a 180deg change of direction on the haul line. The force on the anchor will be greater than the difference of the load and haul force. 

If I knew what a "MA" system was I'd bother to think about it.

Mechanical advantage 

All this is very easy if a complete free body diagram is created. I see "free body diagram" in the title but I don't see any FBDs in the discussion. I taught Statics at university for 30 years and I am certain that if you can't get the FBD right, you can't solve the problem.

Jim Titt is correct in his comments.

Dan Merrick wrote:

All this is very easy if a complete free body diagram is created. I see "free body diagram" in the title but I don't see any FBDs in the discussion. I taught Statics at university for 30 years and I am certain that if you can't get the FBD right, you can't solve the problem.

Jim Titt is correct in his comments.

I just did, and it’s still not correct. For some reason, I can’t attach pictures from my phone so I’ll add the diagram later.

It’s also possible I’m misinterpreting what Jim said

Edit: maybe this is what Jim meant to say. The load on the anchor is always the SUM of the load force and hauling force ( understanding that the hauling force can either be positive or negative, depending how the system is configured). 

Dan Merrick wrote:

All this is very easy if a complete free body diagram is created. I see "free body diagram" in the title but I don't see any FBDs in the discussion. I taught Statics at university for 30 years and I am certain that if you can't get the FBD right, you can't solve the problem.

Jim Titt is correct in his comments.

Nothing quite like a “real” teacher swooping in to flex while adding nothing of merit to the discussion. 

In the model that I made, JTP (Jimm Titt's Prophecy) holds true: "In any system hauling from above the load on the anchor is always the load force minus the hauling force no matter what is in between"

This is true in all cases except when I add a parameter for edge friction.  If I add a parameter for edge friction, then the load on the anchor is greater than the load force minus the hauling force. 

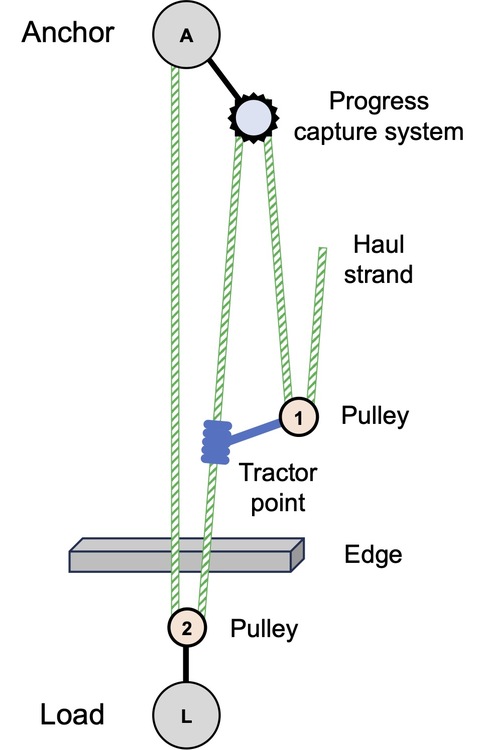
What happens in your system if you add a redirect to the haul line off the same anchor?

Hi Curt, 

So do you mean taking the haul line, passing it through a pulley that is attached to the main anchor, and hauling toward the edge?

If that's what you mean, I can try to work out the numbers.

Also, do you mean taking pulley friction into account, or not?