Impact force calculator?

I am looking for an impact force calculator for an upcoming study. Typically an actuate model would ask for weight, fall factor, top piece friction coefficient (or is fixed at 0.66), and UIAA rope impact force rating. I know JT 512 used to make one, but his website is offline. I need the calculator as a reference for an upcoming mini study I would like to perform.

I found one...

junkfunnel.com/fallforce/

...any others?

There's been a lot of junk on the web (the Petzl and JT512 calculators were good though). I haven't bothered to test it, but it seems likely that the junkfunnel calculator is junk, because it appears to rely on what is typically called the static elongation of the rope, i.e. the rope's elongation under body weight.

If the rope behaved like an ideal spring, you could use the static elongation value to compute the the modulus of elasticity (Hooke's Law constant, Young's modulus, stiffness coefficient, etc, etc) and then use the standard formula to (over)estimate maximum tension for various fall scenarios. But although the tension vs. elongation curve is close to a straight line for a large range of elongations, linearity falls off at the extremes, and the static tension is at the low extreme and so provides a very poor estimate. This assumes that the junkfunnel calculator does the "right" things with the data, i.e. that the only error is in using the static elongation. There are other calculators out there that do the wrong thing after asking for the appropriate parameters, so it is hard to believe any of them.

See the Supertopo thread supertopo.com/climbers-foru… for more on this.

A far better approach is to compute the modulus of elasticity from the UIAA impact rating of the rope. I've described how to do this and written a basic formula with all the usual constant values included in 4sport.ua/_upl/2/1404/Stand… ; you only need a calculator that can take square roots to use this, so no problem incorporating into a spreadsheet.

That said, there is such a spreadsheet on David Coley's companion website ( multipitchclimbing.com/) to his and Andy Kirkpatrick's e-book, High: Advanced Multipitch Climbing which y'all should get! The spreadsheet is at people.bath.ac.uk/dac33/hig… . (Full disclosure: I haven't checked it either. Edit: now I have, and it isn't correct. Endorsement withdrawn...)

rgold wrote:There's been a lot of junk on the web (the Petzl and JT512 calculators were good though). I haven't bothered to test it, but it seems likely that the junkfunnel calculator is junk, because it appears to rely on what is typically called the static elongation of the rope,

That's what I thought at first until I tested it. I plugged in the standard UIAA test parameters and the static elongation of three random ropes, and the calculator was within 0.5kN of the rope's rated impact force for each of the three ropes. One sample was spot-on matching the manufacturer's supplied impact force rating. I am guessing the author was smart enough to realize that the rope does not have a linear stress-strain curve, and he accounted for it.

The problem is that regardless of where you input the measurement (e.g. static elongation, dynamic elongation or UIAA impact force rating), you're still only entering one measurement which is taken at either extremely high impact loads or very low loads. Really, to be truly accurate you would need to take multiple measurements along multiple fall factors to develop a true stress-strain curve, but the calculator seems to be reasonable so far.

Well, I'm surprised that the junkfunnel calculator did that well, but we have no idea what's under the hood...

There are for sure more accurate ways to do this, but all the ones I know rely either implicitly or explicitly on either non-linear differential equations or, more frequently, coupled linear ones, so that rather than a simple formula you need to implement a good numerical approximation routine.

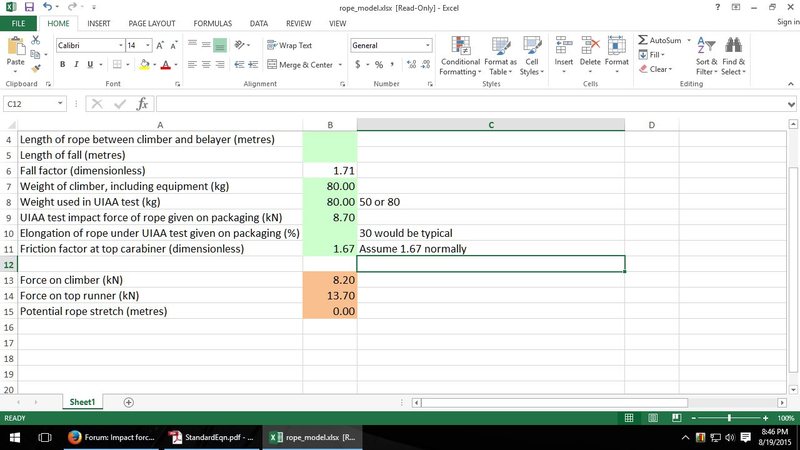
rgold wrote:Well, I'm surprised that the junkfunnel calculator did that well, but we have no idea what's under the hood... There are for sure more accurate ways to do this, but all the ones I know rely either implicitly or explicitly on either non-linear differential equations or, more frequently, coupled linear ones, so that rather than a simple formula you need to implement a good numerical approximation routine.

Maybe it's off, I just tried three ropes.

I like the Excel chart better, thanks. However, it too seems a bit off. I entered 80kg for both weights. 1.71 for the FF, and 8.7 for the impact force rating. I received 8.2kN out of the calculator for the load on the climber. I should have received 8.7kN as I entered in the exact parameters of the UIAA test scenario.

I think if you want to get the UIAA impact rating back out you might have to set the top carabiner friction factor to zero.

rgold wrote:I think if you want to get the UIAA impact rating back out you might have to set the top carabiner friction factor to zero.

That value only modifies the load on the top piece. The load on the climber remains the same.

rgold wrote: That said, there is such a spreadsheet on David Coley's companion website ( multipitchclimbing.com/) to his and Andy Kirkpatrick's e-book, High: Advanced Multipitch Climbing which y'all should get! The spreadsheet is at people.bath.ac.uk/dac33/hig… . (Full disclosure: I haven't checked it either.)

My spreadsheet is ok for what is designed to do - teach people about some of the relevant parameters and their impact. As an accurate tool for real falls it isn't up to the job. But then, I'm not sure what is as friction on the rock etc. and the belayer are key.

One can see this down the climbing gym. Lots of people, same ish rope, some people get slammed, other fall softly

We understand that David. The essential nature of any model is that it ignores some features of reality, otherwise the model would be the real thing. The question I raised is whether the model effectively implements whatever physics underlies it.

After looking at the spreadsheet, I'm afraid I'm not buying the formulas in it, which aren't fully justified in the discussion of physics on the site and seem to be assuming more linearity than is present. A way to see the formulas have to be wrong is to check their result for fall factor=0, i.e. just weighting the rope. The maximum tension should be twice bodyweight (this doesn't seem to be well-known), but the spreadsheet formulas give 0 tension, which of course can't possibly be right no matter what your rope model is.

Another aspect of the spreadsheet is that it imposes a 25% increase to the test weight. In other words, if you input a 80kg test weight, the spreadsheet uses 100 kg (the discussion on the site says 90kg by the way). The reason for this is an assumption that an 80kg steel weight produces results we'd see from a 100kg squishy body. This may well be a reasonable approach to getting relevant numbers, but obviously you can't get the UIAA impact numbers back out if they are being internally modified in the calculations.

Although not relevant here, the site also gives the UIAA test weight for half ropes as 50kg, but the correct figure is 55kg.

Here, from the note I wrote and referenced earlier, is the standard formula, based on the model of the rope as an undamped simple harmonic oscillator. Almost all the more sophisticated models still take this as their starting point.

T = 0.718 + sqrt[ 0.615 + 0.562*U*(U-1.568)*r ]

Here T is the maximum tension in the rope in kN, U is the UIAA impact force in kN, and r is the fall factor. It is easy enough to enter this into a spreadsheet, and as things stand now I'd say this is your best bet.

(I want to emphasize that the formula itself has been known to climbers for about 60 years and there is nothing original in my account, it is simply an exposition of known facts.)

I should add that I used the value r=1.78 as the UIAA fall factor. There seems to be some confusion about this; a quick look at the web reveals that Edelrid (and multipitchclimbing.com spreadsheet) use 1.71, Mammut says 1.75, and Petzl says 1.77. Precise information is available from EN 892, which costs two hundred or so dollars to consult. A diagram published by the UIAA of the test procedure does not settle the question, since there is a turn of rope at the top of the diagram with no measurements given. In any case, these small variations in the UIAA figure probably only effect the second decimal place in the final answer.

rgold wrote: In other words, if you input a 80kg test weight, the spreadsheet uses 100 kg (the discussion on the site says 90kg by the way). The reason for this is an assumption that an 80kg steel weight produces results we'd see from a 100kg squishy body.

That's a bit silly considering no one is going to enter in their own weight into the calculator as an estimated rigid-weight equivalent. They are going to enter in whatever they weigh. However, on a side note, when I entered in 80kg, the calc was only off by about 0.5k. However, if I bump it down to around 65kg to account for a 25% increase, then the calculator is even further off, missing the target number by about 2kN.

While the UIAA diagram does show a loop of slack in the rope, it still gives the total fall distance values, and when plugging those numbers in we get FF 1.71. One could always just email the UIAA and ask.

Also, your formula does not account for weight, which is required to determine impact force. Or are you assuming 80kg as the UIAA uses?

I edited my response above to give further evidence that the formulas are just plain wrong.

Sorry, I forgot to mention that my formula assumed an 80kg leader. You want an analogous formula with a variable for the leader's weight?

Yes, the UIAA diagram gives the total fall distance; what is unclear because of the loop at the top is the total amount of rope in the system, so it is not obvious what the fall factor should be. The fact that three randomly-consulted rope manufacturers seem to have different values seems to confirm this ambiguity. I don't see how you get ff=1.71 from what's in the diagram I have. It appears to me that the fall height is very clearly 4.8m. To get ff=1.71, you'd need 2.8 m of rope in the system; I only see 2.6m explicitly accounted for. (Because of dumbness. Rocknice2 'splained below.)

Your objections to the weight modification aren't on point, because the calculations in the spreadsheet use the ratio of the climbers weight to the test weight, and I would guess that the reasoning is that the ratio should either be a ratio of squishy weights or a ratio of steel weights. The climber's weight is a squishy weight, so the 80kg test weight is converted to a purportedly equivalent 100 kg squishy weight. The result is to lower the impact force calculated, as you would expect when taking account of energy-absorbing effects of squishiness. But all this is moot, because the linearity inherent in the use of these ratios is incorrect, as the fall-factor zero example ought to make clear.

In the diagram there is 2.8m of rope in the system. 2.5m down to the weight and .3m to locking pin. The weight of raised 2.3m above ring giving you .2m of slack.

I'd it possible that the length of 2.5m is measured with the weight resting on the rope. Therefore stretching it slightly? IDK.

Oh---right you (and 20kN) are! Forget about the business about the loop of rope. So this means I ought to modify the numbers in my formula so that ff=2.71, not 2.78. Will do...ok, here we go:

with

T: maximum rope tension in kN.

w: climber weight in kN.
(80 kg is climber mass. It has to be multiplied by g = 0.0098 to get w=0.784 kN)

k: rope modulus, here computed from the UIAA impact force.

r: fall factor.

U: UIAA impact force in kN.

UIAA impact force fall factor is taken to be 1.71.

By the way, the method used in the multipitchclimbing.com site implicitly assumes the formula



for some constant C. Compare to the correct formula above.

Both the e-book and the site are fantastic resources. It's just the rope model section and the spreadsheet that need revision.

rgold wrote:You want a formula with a variable for the leader's weight?

Yes, since I dont weigh 80kg. The idea is to input the weight, UIAA impact force value, and FF, an assumed carbiner friction value of 0.66, and then get the theoretical maximum impact force on the top piece out of the calculator.

The formula just above does that, using the undamped spring model for the rope. Put it in your spreadsheet and you're good to go. Don't forget to multiply your mass in kg by 0.0098.

Nothing in the formula has to be taken on faith; all the arguments, assumptions, and details are in the article I linked earlier.

rocknice2 wrote:In the diagram there is 2.8m of rope in the system. 2.5m down to the weight and .3m to locking pin. The weight of raised 2.3m above ring giving you .2m of slack. I'd it possible that the length of 2.5m is measured with the weight resting on the rope. Therefore stretching it slightly? IDK.

The weight is hung on the rope first to tighten the knot. You can´t raise the weight 2.5m above the pin due to it´s physical size since it is usually a sizeable concrete block and the pin has to be to the side to let the weight fall past.

rgold wrote: By the way, the method used in the multipitchclimbing.com site implicitly assumes the formula for some constant C. Compare to the correct formula above. Both the e-book and the site are fantastic resources. It's just the rope model section and the spreadsheet that need revision.

I'm always happy to make improvements

David Coley wrote: I'm always happy to make improvements

Well the calculator should match the UIAA spec of a rope. If you put 80kg in, 1.71FF and an impact force of 10kN, the output should obviously be 10kN.

20 kN wrote: Well the calculator should match the UIAA spec of a rope. If you put 80kg in, 1.71FF and an impact force of 10kN, the output should obviously be 10kN.

This might be viewed as necessary, but it is far from sufficient. The current incorrect multipitchclimbing.com formula would reproduce the UIAA numbers if it didn't also have the squishy body correction, as would an infinite number of other formulas that don't have anything to do with rope behavior.

The standard equation itself is not accurate as a representation of what happens in the field and isn't good for much more than David's original goal, which is to "teach people about some of the relevant parameters and their impact."